Scholarly teaching. Education research. Scholarship of Teaching and Learning. These are all activities related to applying valid research methods – typically developed in other disciplines – to study teaching and learning.
For faculty members who’s merit, tenure, and promotion is based, in part, on their research output, publishing articles about education can’t hurt but it may not be seen as important as their disciplinary research. UBC, like a growing number of universities, has a tenure-track stream of Assistant, Associate, and (full) Professor of Teaching. We call it the Educational Leadership stream because success and promotion requires demonstrating impact and leadership beyond your classroom. For faculty in this stream, engaging in SoTL is a powerful way to demonstrate that leadership.
It’s my Centre for Teaching and Learning’s mission to “promote, inspire, and support excellence, leadership, scholarship, and technologies in teaching and learning.” I find supporting scholarship is one of most difficult part of our mission because when we start talking about research, each faculty member immediately snaps to the kinds of disciplinary research they do – if any – and tries to force education into that methodology. I struggle to support them because (i) I don’t know what kind of research they do and (ii) I’m most familiar with research methods found in STEM.
I’m writing this post because something happened last week, something good, that’s changed my approach and, I hope, the success of the faculty members I work with. Here’s the story. Dr. Jasmin Hristov, a research-stream Assistant Professor in the Department of History & Sociology, Irving K. Barber School of Arts and Sciences gave me her permission to tell it.
Professor Hristov teaches upper-level sociology. She plans to bring in a series of guest speakers via video conference and asked if she could use my Centre’s workshop room. “Yes, of course,” I replied. And then, thinking about my Centre’s mission, I added, “You’re doing something innovative – would you be interested in talking about how you could study whether or not it’s effective?” She was, and we met.
First, Professor Hristov described her motivation: introduce the students to six experts from around the World, with careful attention to diversity of gender, race, location, and rank. For each guest speaker, the students do some background reading, prepare questions to ask the speaker, and lead a discussion. After class, the students write a reflection about the experience.
“How can we tell if it was effective? How can we tell if students learned anything?”
We nearly got lost down a dead end. Professor Hristov: “I’ve taught this course before without the video conferencing but with different students and, obviously, without the reflection.” Both of us nearly concluded, “Without a control group to compare grades against, I don’t see how we can study this.”
We didn’t go there, though, because serendipitously, I started the conversation with,
How can we find evidence of impact?
This question opened up whole new ways of thinking, without sending us on that narrow “research = A/B study with statistical significance” path. It led quickly to a couple of possibilities that could produce interesting results that don’t rely on the success or failure of p < 0.05.
Text analysis of students’ reflection
4-page reflection × 6 reflections × 30 students = huge amount of text
Imagine examining all that text with powerful tools like Voyant or NVivo. Will students naturally comment on the diversity of the speakers? That was one of the elements deliberately built into this intervention, recall. Do they need a prompt? Not a heavy prompt like, “Please comment on the diversity of the speakers.” That will only get the answers the students think Professor Hristov wants to hear. Something more subtle, like, um, not sure yet.
But imagine the kind of evidence of impact she could include in the SoTL article:
“I carefully chose the speakers to expose my students to a wide range of races, locations, genders, and ranks. In their reflections, students made the following associations…”
This isn’t cherry-picking an individual student’s comments – that’s a helpful exemplar or supporting anecdote but it’s not evidence. Instead, we have legitimate connections and insight students are making.
Quantitative analysis of reflection grades
Just because we can’t do a controlled A/B study doesn’t mean we can’t do quantitative analysis. Imagine this: imagine we compare the students’ marks on the reflections with their marks on the rest of the course. The reflections are worth around 1/3 of the total mark, so the reflections are worth enough that students will put legitimate care and effort into them. In other words, the reflections are not some incidental marks students can blow off, and they’re not so important that nothing else matters in the course. I made up some data (thx, RANDOM.org) to see what kinds of conclusions we could make (click to enlarge):
The left graph shows there’s a relationship between the students’ success on the reflections and the rest of the course. Do the reflections help them succeed with the other assignments? Do the other assignments help them write better reflections? Can’t tell. Better look at the text analysis…
The center graph isn’t telling a compelling story. Success on the reflections doesn’t seem to have any connection to success on the rest of the course. We can probably conclude the same about what the students are getting out of the video conferences. Time to rethink how the video conferences are integrated and supported.
The right graph is a worst-case scenario: success on the reflections comes at the expense of the their success in the rest of the course. Oh c’mon, this would never happen, right? Well, I’ve seen courses where there’s a “capstone project” that takes all the students’ time. If the capstone is that important, it should probably represent a significant fraction of the overall course mark, so success on the capstone guarantees success in the course. I’ve also seen cases where success on the capstone requires sacrificing the other courses you’re taking – time for the Department Head to get the course instructors together to coordinate their assignments!
No matter the scenario, there’s something here for Professor Hristov to share in the discussion of her SoTL paper. The conclusions will be useful to others thinking about integrating video conferencing into their courses.
Evidence of Impact
This will be my new conversation starter when promoting, inspiring, and supporting scholarship. It’s also a good prompt for the faculty members, themselves, who want to (need to?) demonstrate educational leadership. This prompt invites us to be curious and creative, instead of trying to jam teaching and learning into the same research methods that we’re familiar with from disciplinary research.
The President’s Council of Advisors on Science and Technology (PCAST) forecasts “a need for producing, over the next decade, approximately 1 million more college graduates in STEM fields” and makes 5 recommendations for reaching this goal:
In May, 2013, the Committee on STEM Education (CoSTEM) within the National Science and Technology Council released, “Federal Science, Technology, Engineering, and Mathematics (STEM) Education 5-Year Strategic Plan.” The report recommends 5 areas for STEM Education investment:
In 2012, the National Research Council published the Discipline-Based Education Research (DBER) Report. It describes how each of the STEM disciplines can address 3 key issues:
4. Reaching Students by Nancy Kober (2015)
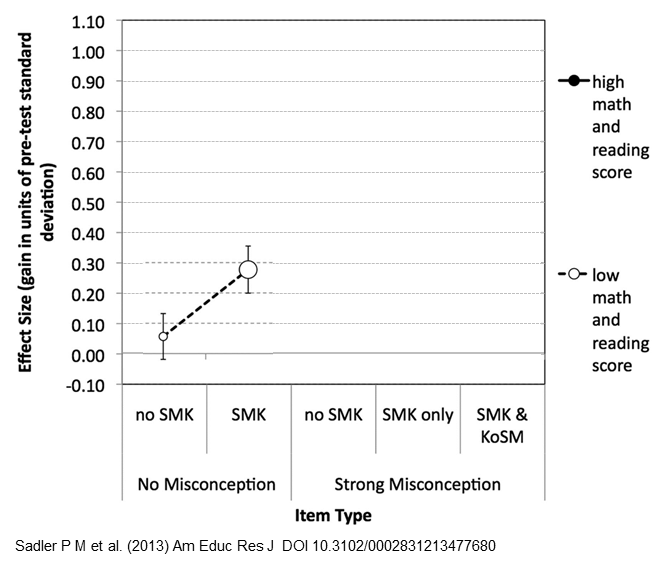
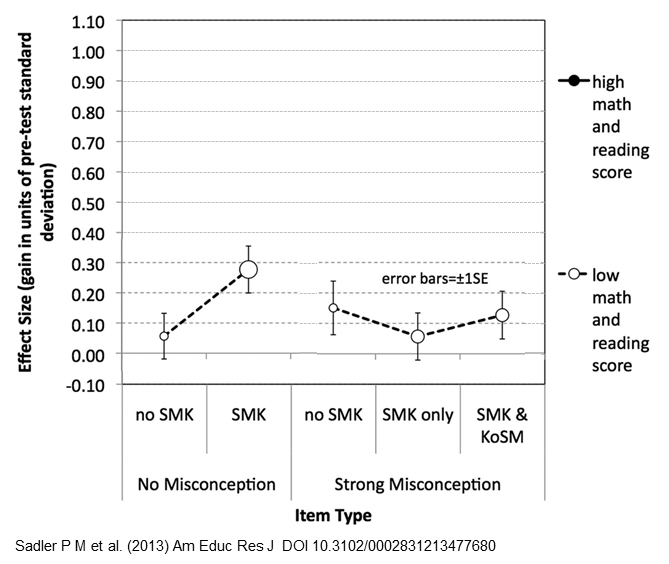
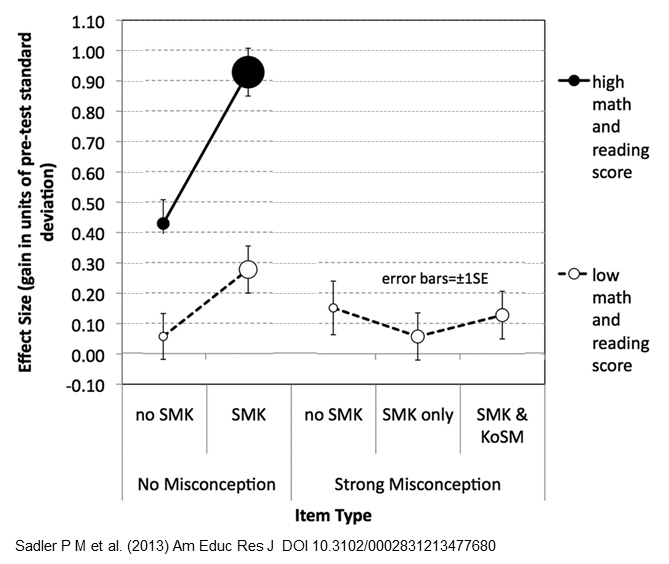
![Let's look at the axes of the graph first, before the data blind us. (Adapted from [1])](https://peternewbury.org/wp-content/uploads/2018/03/SadlerMisconceptionGraphs_0.png)
